原创: 谭祥军 模态空间
齿轮箱结构的频谱图中经常出现以齿轮啮合频率或其谐频为载波频率,齿轮的转频为调制频率的边频带。这是因为齿轮啮合不精确,载荷和转速不均匀等原因导致了调制现象。调制是指使用调制信号去改变载波信号的一个或几个属性的过程,如可以改变载波信号的幅值、频率或相位等属性。因此,信号调制分三种类型:调幅、调频和混合调制,如图1所示。在这,我们将分别介绍这三种调制类型。
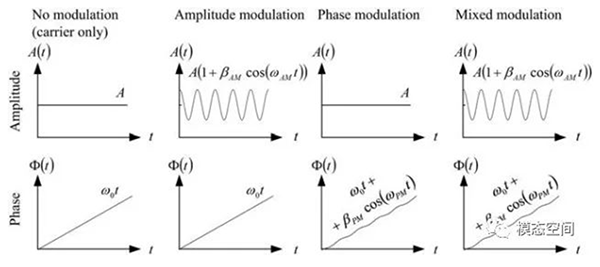
在信号调制过程中,我们要区分载波信号,调制信号和被已调信号。载波信号是指高频的正弦信号或脉冲信号作为信号的载体,如齿轮的啮合频率及其谐波。调制信号是指低频的信号,要用它来改变载波信号的某一个或几个参数,如齿轮的转速信号通常作为调制信号。已调信号是指经过调制之后的载波信号。在这,我们只讨论载波信号是严格的正弦信号的情况。但调制信号不一定要求是正弦信号。对于一般调制信号,叠加原理是有效的,因为调制信号可认为是若干正弦信号叠加组成的复合波形,而每个正弦分量的影响可以分别研究。
1、幅值调制AM
假设载波信号是正弦信号,那么幅值调制信号是载波信号与调制信号在时域上的乘积,转换到频域,则是两个信号的卷积。假设载波信号与调制信号都为简谐正弦波,齿轮啮合频率作为载波信号为
g(t)=Acos(2πfct+φ)
作为调制信号的齿轮的旋转信号为
e(t)=1+βcos(2πfet)
利用积化和差公式展开已调信号为
x(t)=g(t)·e(t)= A(1+βcos(2πfet))cos(2πfct+φ)
= Acos(2πfct+φ)+Aβ/2cos[2π(fc+fe)t+φ]+Aβ/2cos[2π(fc-fe)t+φ]
式中,A是载波信号的幅值;β是幅值调制指数;fc是载波频率(齿轮的啮合频率或其谐频);fe是调制信号的频率(齿轮的旋转频率);φ是初相角。
从上式可以看出,已调信号包括三个正弦分量:一个是原始的正弦载波信号,另外两个分别是频率成分为(fc+fe)和(fc-fe)的正弦信号。这两个正弦分量均匀分布在载波信号的两侧,称为上、下边频带。调制不会改变载波信号的幅值,但边频带的幅值等于载波信号幅值与调制指数乘积的一半。上下边频带频率与载波频率的差值为调制信号的频率。
图2给出了一个调制指数为0.5,频率为2Hz的简谐调制信号和幅值为1,频率为100Hz的载波信号的幅值调制结果,左图为时域信号,右图为相应的频谱。分析时选择的参数满足周期性要求,因而选择矩形窗。从图2可以看出,由于调制信号为一个简谐正弦波,因此,频谱图中只有一对边频带。注意图2调制信号的时域波形看起来像拍振的波形,但幅值调制与拍振有着本质的区别:调制是两个正弦信号的乘积,而拍振是两个频率相近的正弦信号的叠加。
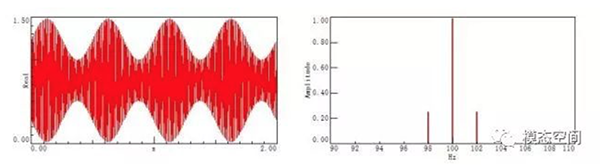
如果调制信号不是一个简谐波,而是由多个正弦波组成的复合周期信号,那么在频谱图中将出现多对边频带(也称为边频族)。这是因为每个正弦成分调制后将产生一对边频带,当有多个正弦成分时,将在载波信号两侧产生多对边频带。
在之前的文章《什么是窗函数》中,我们讲到,为了减少泄漏,需要对不满足FFT变换要求的时域信号施加窗函数,加窗过程示意如图3所示。加窗的过程是原始的时域信号与窗函数在时域上的乘积,因此,施加窗函数的过程属于幅值调制。如当施加汉宁窗时,一个周期的余弦信号为调制信号,调制指数等于1。如果简谐信号的频率成分与频谱图中的某些频率匹配,那么施加窗函数之后,将在频谱图中出现幅值为原来幅值一半的一对边频带。其他类型的窗函数将出现多对边频带,如平顶窗可能将出现多对边频带,这是因为平顶窗是多个余弦函数之和。
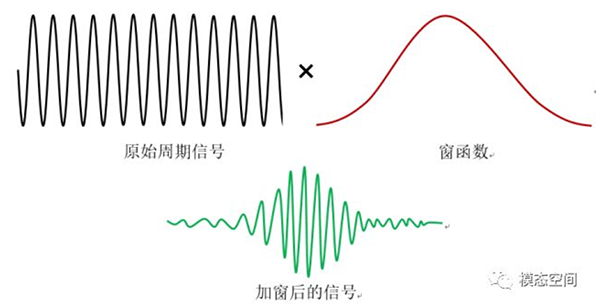
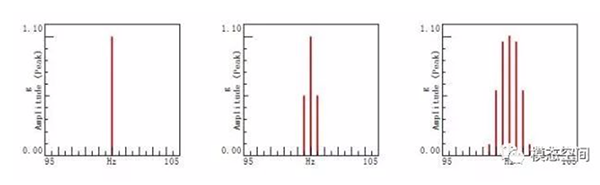
图4为一个单位幅值,频率为100Hz的正弦波加不同窗函数得到的频谱。频谱计算所用的频率分辨率为0.5Hz,因此,图4左侧为加矩形窗得到的频谱为单一谱线。图4中间为加汉宁窗的结果,汉宁窗为一个周期的余弦函数,调制指数为1,因此,频谱结果中出现了一对边频带,幅值为0.5。图4右侧为加平顶窗的结果,频谱图中出现了多对边频带。因此,时域加窗过程实旨是幅值调制过程,边频带的出现才体现了能量泄漏。另一方面,幅值调制会改变信号的总能量,使得已调信号的幅值忽大忽小。在加窗的过程中,由于窗函数改变了信号中的能量,所以,需要进行修正。
当齿面上的载荷波动、齿轮加工误差(如齿距不均匀)、齿轮偏心以及齿轮故障所产生的局部性缺陷和均布性缺陷等情况时易引起幅值调制。根据边频带的形状,可以分辨出齿轮存在局部性缺陷还是分布性缺陷。
如果发生断齿或大的剥落等局部性缺陷,当啮合点进入缺陷处时,相当于齿轮的振动受到一个短脉冲的调制,脉冲的长度等于齿轮的啮合周期。齿轮每旋转一周,脉冲就重复一次。由于脉冲可以分解为多个正弦分量之和,因此在频谱图上形成以载波频率及其谐频为中心的一系列边频带。其特点是边频数量多、范围广、数值小、分布均匀且较为平坦,并且每一个边频之间的间隔等于齿轮的旋转频率。
如果在齿轮上存在点蚀、划痕(胶合)等分布比较均匀的缺陷,调制频率的成分虽然较多,但在时域上是一条幅度变化较小、脉动周期较长的包络线,因此频谱图上边频带的特点是分布比较高而窄,而且幅值变化起伏较大。
2、频率调制FM
频率调制是指载波信号受到调制从而形成的变频信号,表现为时域波形疏密的变化。对于一个正弦信号Asin(2πft+φ)而言,其相位Ф(t)=2πft+φ,因此,相位与频率有对应关系,所以频率调制也可以认为是相位调制。
假设齿轮啮合的载波信号为
g(t)=Acos(2πfct+φ)
作为调制信号的齿轮的旋转信号为
e(t)=βcos(2πfet)
则频率调制信号可描述成
x(t)=Acos(2πfct+βcos(2πfet)+φ)
已调信号的相位Ф(t)= 2πfct+βcos(2πfet)+φ,其频率为
f(t)=(1/2π)(dФ/dt)= fc-βfesin(2πfet)
βfe表明了频率调制的频率偏离范围,从上式可以看出,频率调制时,应有fc>βfe。上式中,A是载波信号的幅值;β是频率调制指数;fc是载波频率(齿轮的啮合频率或其谐频);fe是调制信号的频率(齿轮的旋转频率);φ是初相角。
已调信号x(t)=Acos(2πfct+βcos(2πfet)+φ)根据第一类贝塞尔函数,可展开成奇数顶,偶数项和零项:
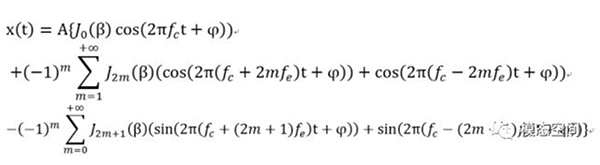
式中,Jn(β)是以β为自变量的第n阶贝塞尔系数,n=0,1,2,3,…。从上式可以看出,除了载波频率fc之外,频谱图中将出现无穷多对间隔为调制频率fe的边频带。
图5为一个载波频率为100Hz,调制频率为5Hz,调制指数10的已调信号的时域波形(上)和相应的频谱(下)。由于所选参数满足FFT变换的周期性要求,因此,频谱计算时应用矩形窗。从时域波形上可以看出,已调信号的幅值没有变化,但疏密程度变化明显。由于调制指数为10,因此,频率调制的频率范围为100±50Hz,从图中可以看出,边频带主要集中在50Hz到150Hz之间。频谱幅值主要位于前200Hz带宽内,但注意到载波信号的幅值不占主导地位。
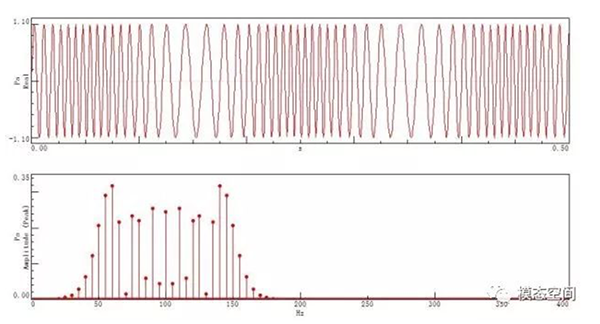
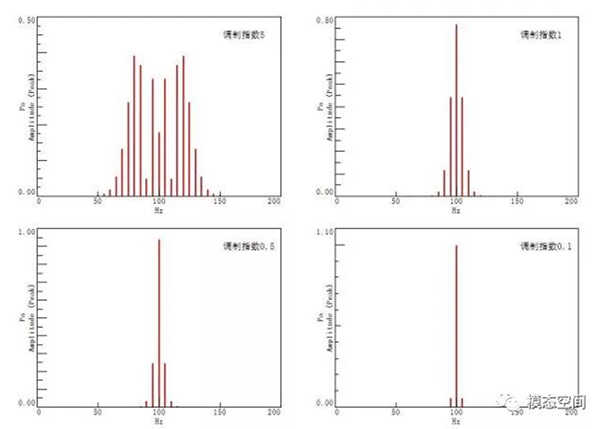
图6为载波频率为100Hz,调制频率为5Hz,在不同调制指数下的已调信号的频谱图。从图中可以看出,调制指数越大,边频带对数越多,对应的谱线幅值越低。这是由于频率调制并不改变信号的总能量,调制指数大时,对应的谱线多,这相当于载波信号的能量分散到边频带上了,所以,谱线越多,每条谱线上的幅值越小。
在升降速工况下,对旋转机械进行瀑布图分布时,跟踪变化的转速做频谱计算时,可以认为是频率调制的例子。在一块时域数据块内,输入轴的转速(用于跟踪)从这块数据的开始时刻增加或降低持续到数据块末端,转速的变化引起转频的变化,从而引起频率调制,此时可认为以数据块起始时刻的转频作为载波频率,频率变化速率为调制频率,如每秒钟转频变化10Hz。由于边频带的出现导致瀑布图分析时频率拖尾严重,导致瀑布图中阶次不清晰。
对于齿轮啮合,由于所受的扭矩不均匀,从而引起转速波动;另一方面,齿轮加工时存在齿距误差,因此,这两方面都会引起啮合速率的变化从而产生频率调制现象。
3、二者的异同
幅值调制和频率调制有一些共同之处,也存在明显的差异。对于齿轮啮合的幅值调制和频率调制而言,二者均以啮合频率或及谐频作为载波频率,以齿轮的旋转频率作为调制信号的频率,因此,两类调制有相同的载波频率和调制信号的频率。由于调制信号的频率相同,所以,两类调制产生的边频带的间隔是相等的。且边频带都对称分布于载波频率两侧。但是,如果幅值调制的载波信号和调制信号均为正弦波,则只产生一对边频带,而此时的频率调制将产生无穷多对边频带。
两类调制都有调制指数这个概念,但幅值调制指数影响的是已调信号的幅值大小,而频率调制指数影响的是边频带的分布。
对于载波信号是正弦波而言,幅值调制导致信号的幅值忽大忽悠小(见图2),因而,幅值调制会改变信号中的能量。加窗属于幅值调制,因为窗函数改变了原始信号的能量大小,所以,需要进行修正。但频率调制只是改变载波信号的疏密,不改变幅值(见图5),因此,频率调制幅值大小不变,不改变信号中的能量。
4、混合调制
以上考虑的只是单种类型的调制,实际上,齿轮故障缺陷造成的齿面载荷波动,在产生幅值调制的同时,还会造成扭矩波动,导致角速度变化而形成频率调制。因而,实际啮合的齿轮既存在幅值调制,又存在频率调制。在这我们考虑以下情况:两类调制的调制频率相同时相位不同;以及相位相同时调制频率不同。
图7为载波频率为100Hz,调制频率均为5Hz,幅值调制指数为0.5,频率调制指数为3时的同相位和相位偏移90度时的时域波形和频谱图。图7中左侧的图为调制信号的初相位均为0度时的时域波形和频谱,可以看出,当初相位相同时,频谱中的边频带关于载波频率呈对称分布。图7右侧的图为二者相位相差90度时的时域波形和频谱图。当相位相差90度时,时域信号的疏密也不对称了,此时频谱图中的边频带不再关于载波频率呈对称分布。
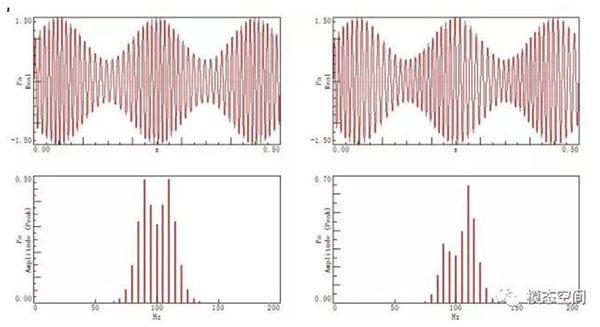
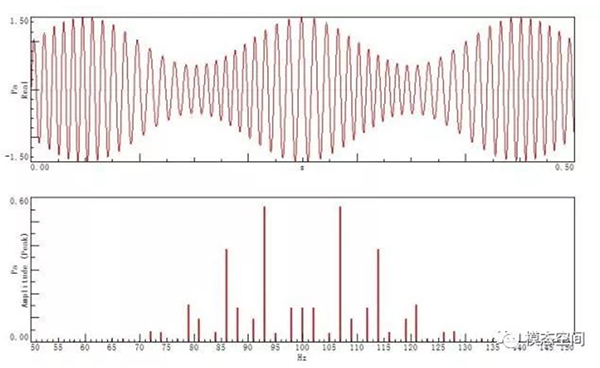
图8为载波频率为100Hz,幅值调制信号的频率为5Hz,幅值调制指数为0.5;频率调制信号的频率为7Hz,频率调制指数为3时的同相位的时域波形和频谱图。频谱图中的边频带仍关于载波频率呈对称分布,但边频带的间隔除了5Hz和7Hz之外,还有它们的和频或差频。为了突出显示这个频带,图中显示的频率区间为50~150Hz。3对高幅值的边频带对应的频率为7Hz,幅值调制只有一对边频带,出现在95Hz和115Hz处。其他的边频带均为两个调制信号的和频或差频,同时,注意到在频率调制的边频带两侧出现了间隔为2Hz的边频带,这是交叉调制的结果。
在实际的齿轮故障诊断中,不会存在单一类型的调制,而是存在混合调制,这将导致边频带呈现出非对称性。另一方面,由于啮合的齿轮的输入转频与输出转频相差不大,因此,这一定程度上会增大交叉调制的可能性,会给齿轮故障诊断带来更大的困难。
参考:
1. Jiri Tuma,Vehicle Gearbox Noise and Vibration: Measurement, Signal Analysis, Signal Processing and Noise Reduction Measures. John Wiley & Sons, Ltd, 2014
本文转自:齿轮的调制效应





