原创: 谭祥军 模态空间
根据完美的齿轮传动,两个啮合的齿轮的转速之比等于齿数比的倒数。如图1所示的齿轮,大齿轮50个齿,小齿轮25个齿,假设大齿轮的转速为100rpm,如果是完美啮合,那么小齿轮的转速将是200rpm。但是因为传递误差的存在使得小齿轮的转速将不是200rpm,从而使得动力传递不平稳。

对于完美的齿轮啮合,齿轮对应该满足以下条件:几何完美,对中完美,刚度无限大。这样才能保证啮合点的线速度相等,即ω1R1=ω2R2。但实际因齿轮变形、装配问题或啮合刚度的变化等原因将导致齿轮啮合时,ω1R1≠ω2R2,存在传递损失,也就是所谓的传递误差。传递误差普遍存在于齿轮传动、皮带与皮带轮传动等传动装置中,是用来描述传动不平稳性的参数。
1 、传递误差的定义
传递误差定义为旋转结构(如齿轮或皮带与皮带轮)的角位移或角速度(转速)与理论值之差。也可以表示成相对于驱动轮(或轴)的绝对值或相对值。
用角位移绝对值定义:
Te=θ2-Tr*θ1 或者 Te=θ1-θ2/Tr
用角位移相对值定义:
Te=(θ2-Tr*θ1)/θ2 或者 Te=(θ1-θ2/Tr)/θ1
用角速度绝对值定义:
Te=rpm2-Tr*rpm1 或者 Te= rpm1- rpm2/Tr
用角速度相对值定义:
Te=(rpm2-Tr*rpm1)/rpm2
或者
Te= (rpm1- rpm2/Tr)/rpm1
其中,Te表示传递误差,θ1和θ2分别表示轮(或轴)1和2上测量的角位移,rpm1和rpm2分别表示轮(或轴)1和2上测量的角速度,Tr表示二者的传动比。如果传递误差为0,则说明没有传动损失,属于完美传动。
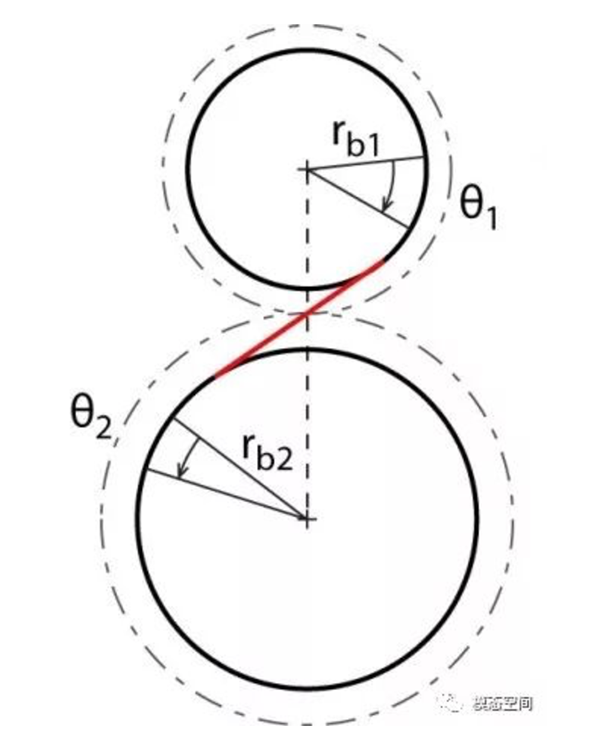
传递误差描述运动学上的运动传递的偏离量,被广泛认为是一种可靠的度量尺度。对于齿轮啮合而言,它描绘因齿轮啮合产生的内部和外部激励共同作用的结果。通常,如果用绝对角位移来描述,如图2所示,传递误差的量级可能只是毫度级或更小。这时对应的绝对位移误差近似表示如下
Te位移=rb1*θ1-rb2*θ2
从上式可以看出,位移误差极其小,可能量级是微米级。因此,对于表示极小的幅值,则要求极高的精度。
2、产生的可能原因
分析传递误差需要从两个方面着手,一个方面与齿轮的几形变形相关;另一方面与齿的啮合相关。也可以按静态误差和动态误差来分类。静态误差主要是指齿轮制造误差和几何误差,而动态误差是指啮合过程中受到周期变化的作用,如啮合刚度的变化,载荷的变化,温度的变化等。
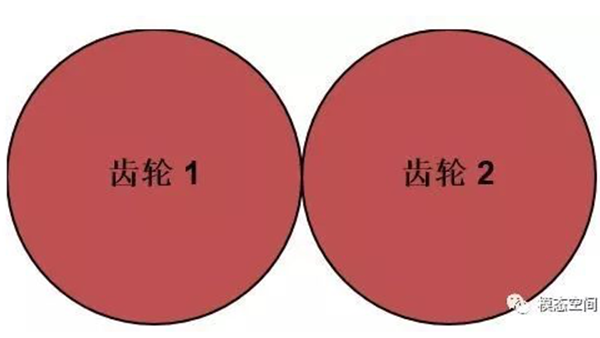
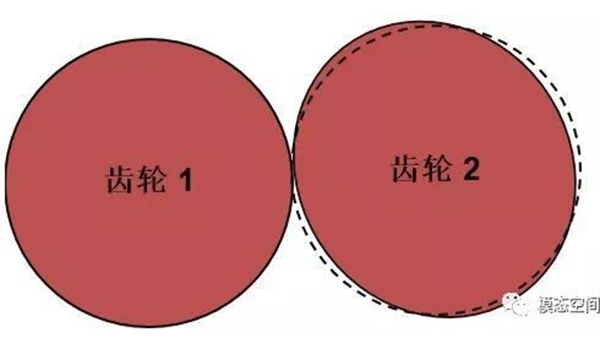
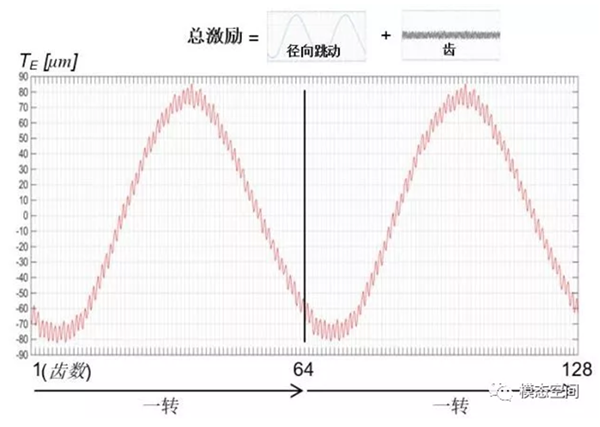
对于完美啮合的齿轮而言,不存在几何变形,偏心或对中等问题,如图3所示。但是由于制造误差等原因将导致齿轮偏心或几何变形,如变成了椭圆,如图4所示,虚线表示完美的齿轮。齿轮几何形状的变化将导致齿轮啮合时存在径向跳动,径向跳动周期相对于啮合周期而言,周期更长,因此,是一种低频的运动,如图5所示。这是一个齿数为64的齿轮的径向跳动波形,从图中可以看出,径向跳动的周期刚好是旋转一圈对应的时间长度。

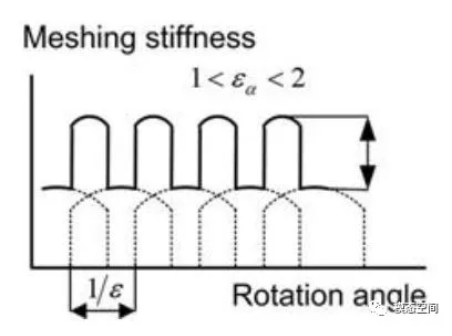
另一方面的原因与齿的啮合相关。在齿轮的啮合过程中,由于主动轮与从动轮的单、双齿啮合交替变换,啮合位置、轮齿啮合刚度(见图6)和载荷的周期性变化(请参考《浅析齿轮结构NVH问题的产生机理》一文)会引起传递损失,从而引起传递误差。另一方面,载荷的不平稳也会引起齿轮本身的刚度变化。
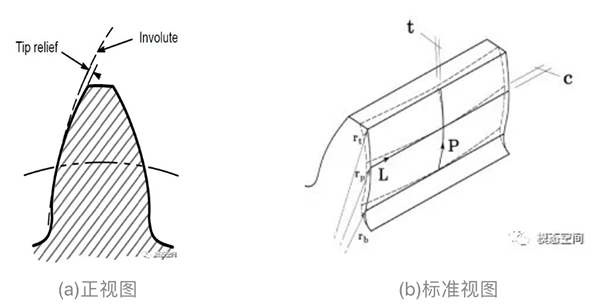
轮齿的形状应该是完美的渐开线,但是由于微观几何误差和制造误差,如图7所示,导致齿面偏离完美的渐开线(图7a)。除了齿面偏离完美的渐开线之外,还会因制造误差导致齿面同一高度截面齿厚不一致(图7b),这些制造误差都会对传递误差有贡献。
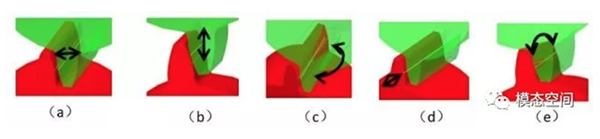
齿轮在装配过程中,可能会存在如下的装配误差(如图8所示):对中误差、角度误差、装配公差和结构变形等。如装配后两齿轮的节圆线周向(图8a)和径向(图8b)有偏离、节圆线周向(图8c)和径向(图8e)有夹角、轴向有偏离(图8d)等装配误差。这些装配误差对传递误差同样有贡献。
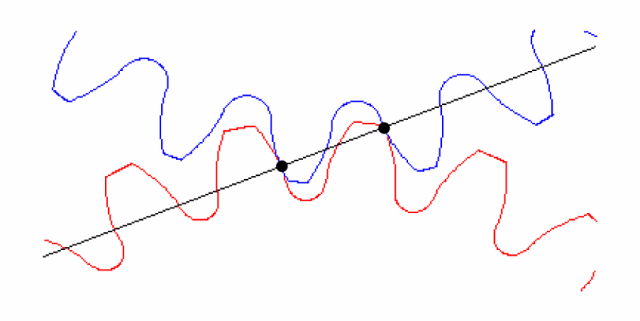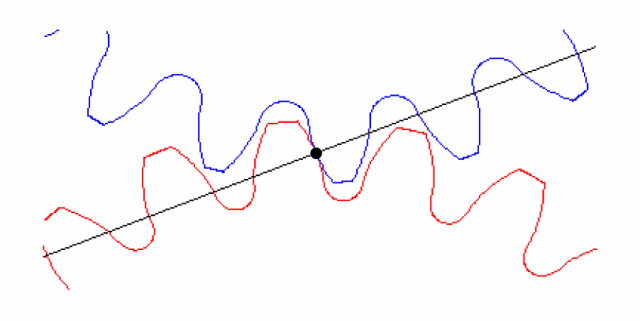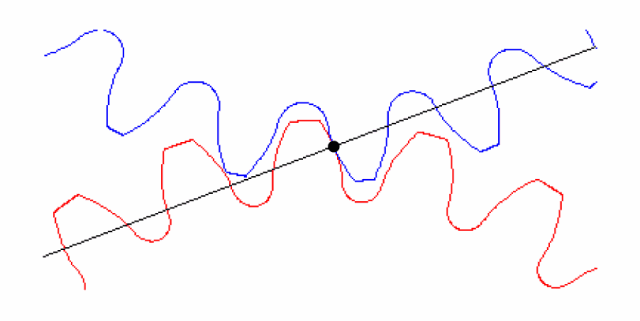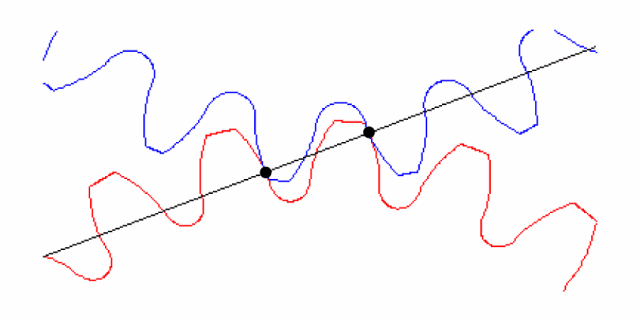
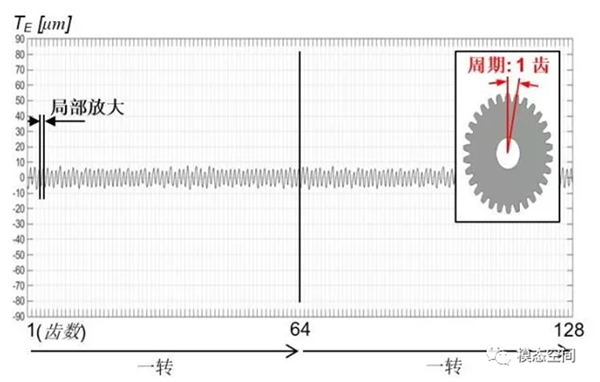
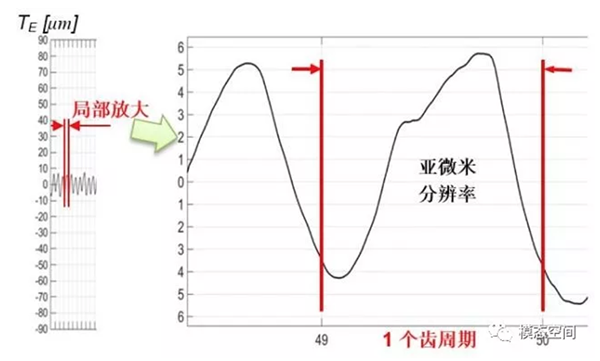
轮齿和齿轮刚度的变化、轮齿微观几何误差、制造误差和装配误差等方面都对齿轮的传递误差有贡献。这些误差造成的传递误差以1个啮合周期为周期,而齿轮的啮合频率高,因而这些误差导致的传递误差是一种低幅值高频的传递误差,如图9所示。局部放大一个齿周期内的传递误差信号,如图10所示,可见,传递误差幅值量级特别小,因此,要分辨出这些传递误差,要求极高的分辨率。另一方面,由于是啮合过程产生的传递,因而,这些传递误差包含了明显的阶次成分。
总的传递误差是两部分误差的叠加,即径向跳动激励和啮合激励的总和。径向跳动激励对应的传递误差是一种高幅值的低频长波,以旋转周期为周期,如图5所示。而啮合激励是一种低幅值的高频短波,以齿轮啮合周期为周期,如图9所示。这两部分的总贡献如图11所示。
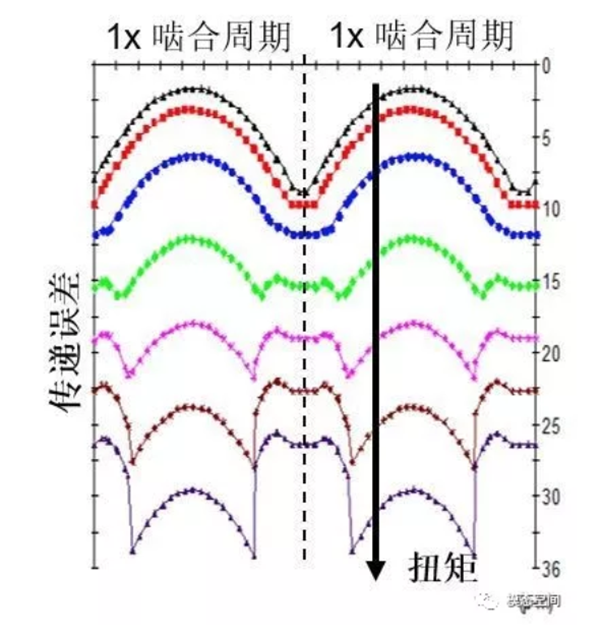
除了齿轮自身的制造误差和几何误差等静态误差之外,齿轮还受到的动态误差的作用,这些误差包括齿轮在工作过程中因温度变化引起的变形和载荷变化引起的弹性变形。齿轮受到的载荷的变化对传递误差也有影响。齿轮受到的载荷为扭矩,当传递的载荷不平稳时(如发动机输出的扭矩有波动),会造成转速波动,波动的转速会加剧传递误差。另外,扭矩的大小对传递误差也有明显的影响,如图12所示,扭矩越大,传递误差幅值越大,幅值变化越显著。
3、产生的影响
当齿轮啮合存在明显的传递误差时,导致齿轮传动不平稳,传递效率将会大大降低,从而影响结构的性能。另一方面,传递误差对结构的NVH性能有着重要的影响。
我们知道啮合齿轮产生了传递误差,将使得啮合齿轮之间的摩擦加剧,这种加剧的摩擦将引发明显的齿轮啸叫。齿轮啸叫属于内部激励,归因于啮合刚度变化和几何误差,产生的是单频噪音,与阶次相关。除了啮合啸叫之外,还会加剧Rattle噪声,当然这是由于外部激励引起的,归因于扭矩波动引起齿相互撞击产生宽带噪声。
4、传递误差分析
根据以上的定义,我们知道计算传递误差需要知道两个齿轮(或轴)的角位移或角速度(转速),还需要知道两个齿轮(或轴)之间的传动比。通常,传动比根据结构特点和啮合关系计算得到。因而,只需要测量齿轮的角位移或角速度即可。而角位移通常难于测量,测量角速度更容易。角速度也就是转速,通过测量转速可以通过后处理得到角位移。故,只需要测量两个齿轮(或轴)各自的转速即可。
获得两个转速信号后,可以按上面定义的公式求得传递误差,可获得绝对角位移误差随时间变化曲线。对传递误差时间曲线做瀑布图分析,可以看出主要的阶次成分和贡献。当然传递误差除了通过试验的方法进行分析外,也可以通过有限元方法进行分析。
本文转自:齿轮的传递误差





