永磁同步电机高频建模方法研究

作者：彭河蒙 胡坚耀 （工业和信息化部电子第五研究所）

1 引言

永磁同步电机具有结构简单、体积小、效率高、损耗小和功率体积比大等优点，目前被广泛应用于新能源汽车的驱动系统。电机作为驱动系统电磁干扰流经的重要路径，建立其高频模型，对下一步搭建系统整体的传导干扰和辐射干扰预测模型十分重要，因此，电机高频模型的精度和准确度会对系统整体模型的精确性和正确性产生很大影响。然而，目前用于建立电机高频模型的方法往往存在建模过程复杂、误差大、通用性差及模型频带覆盖窄等问题，因此，需要一种更为有效的建模方法。

本文首先介绍基于矢量匹配法的电路建模方法：阐述矢量匹配法的基本原理，描述高频等效电路构建过程，推导其模型参数的计算方法。随后用此方法建立星形和三角形两种不同接线方式的永磁同步电机高频电路模型，并进行实验验证。

2 矢量匹配法

2.1概述

矢量匹配法（Vector Fitting）[1]是Gusavsen和Semlyen于1999年提出的一种稳定、有效的拟合方法，该方法避免了有理逼近过程中出现的病态和不平衡加权问题，目前广泛应用于电力系统和高速电路设备频率特性拟合[2-4]，矢量匹配法特别适用于有关频变效应的建模，并在拟合过程中表现出良好的鲁棒性、有效性和稳定性。

2.2矢量匹配法基本原理

电网络理论中，线性电路的网络函数可表达为一有理函数：

(1.1)

可将此函数写成极点、留数形式，即

(1.2)

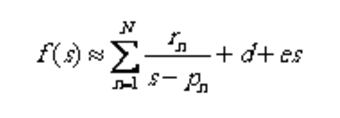
其中，留数和极点是实数或共轭复数对，d和e是实数。

① 矢量匹配法求解过程

给定一组测试数据 (k=1,2…..P)，当极点给定时，式(1.2)就变成关于待求参数、d和e的线性函数，采用矢量匹配法可解出式(3.2)中所有参数、、d和e，其求解过程如下：

设(n=1,2…..N)是函数给定的一组初始极点，同时引入辅助函数，将与相乘，假设与有相同的极点，可得方程：

(1.3)

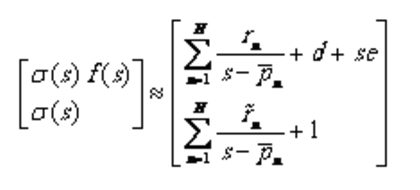
在上式中，有理函数和近似式具有相同的极点，是未知函数的留数，此外，函数的项被强制为1。将式（1.3）中第二行两端同乘并与第一行进行减法运算，可得关于待求参数、、d和e的线性方程。

(1.4)

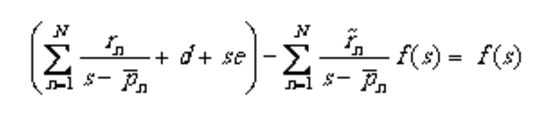
将一组测试数据（k=1,2,3…P）及其对应频点代入(1.4)式，可得一组线性方程，其矩阵形式为

(1.5)

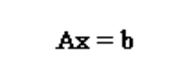
其中，系数矩阵的第k行元素为：

(1.6)

解向量x和已知向量b分别为：

(1.7)

(1.8)

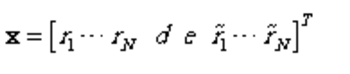
假设第和极点或留数为一组共轭复数对时，形式如下：

(1.9)

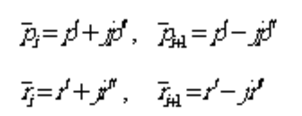
则矩阵中对应元素为：

(1.10)

此时矩阵相应的留数分别是和。

对于式(1.5)一般有，因此它是超定的，可以用最小二乘法求解得到、、和。但是，由给定的初始极点求解式(1.5)计算得到的、和并不准确，因此需要修正初始极点，求解下一次迭代过程中的初始值，使逐步逼近。

用表示式(1.3)第一个方程的右边，将和写成零极点形式有

(1.11)

(1.12)

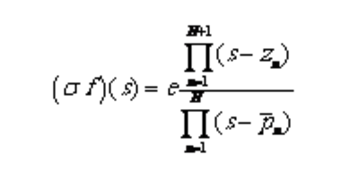
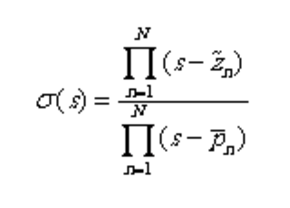
式中，和分别是和的零点。由上式可得

(1.13)

上式表明，的极点与的零点相等。由于有理函数和具有相同的极点，这样，初始极点在运算的过程中相互抵消，求解得到的零点就是下一次迭代的极点。

由式(1.3)和(1.12)可得：

(1.14)

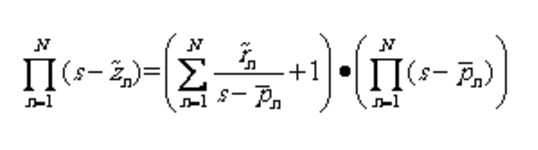
将上式右侧写为行列式形式有

(1.15)

构建矩阵

(1.16)

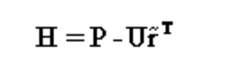
式中，是包含初始极点的对角矩阵，是元素为1的列向量，是包含留数的行向量，即

(1.17)

(1.18)

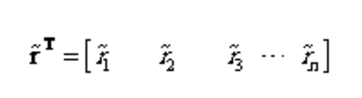
因此矩阵的特征多项式就是式(1.15)，由此，的零点可通过求解矩阵的特征值得到。

当中极点和中对应留数是共轭复数时，各矩阵相应部分的子矩阵为

(1.19)

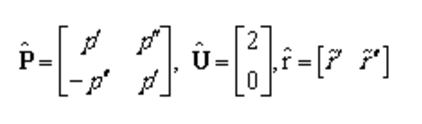
将计算得到的特征值替代式(3.4)的给定的初始极点，再求解式(1.5)。重复这一迭代过程数次，最后得到满足精度要求的、、和。

3 永磁同步电机高频建模

对三相永磁同步电机进行高频建模，本文采用测量法，即把电机看成一个“黑盒子”，不需要知道电机结构和电磁参数，只需测量电机端部阻抗频谱特性，结合矢量匹配法，即可模拟出电机高频电路模型。

电动汽车使用的电机的定子绕组接线方式有两种：星形和三角形，根据电机绕组的连接方式不同，分别对星形接线和三角形接线的永磁同步电机进行高频建模。需要强调的是，在矢量法建模过程中，取为阻抗参数还是导纳参数与定子绕组的接线方式无关，这两个参数是可以相互转换的。

3.1三角形接线电机建模

目前，针对永磁同步电机高频模型研究对象大多数为星形联结的电机，而对定子绕组为三角形联结的电机研究很少。通常，大功率电机的定子绕组接线方式采用三角形联结，这是因为在相同功率下三角形接线较星形接线下绕组中流过的电流较小，可以使绕组线圈制造和布线更为方便。而采用将三角形电机绕组拆卸获取电路参数的方法通用性差，提取过程复杂。因此，有必要对三角形联结的电机高频模型进行研究。

①电机模型

图1三角形接线电机模型

三角形接线电机的高频阻抗网络模型如图1所示，图中，表示三相绕组对地的阻抗，为共模阻抗，表示三相绕组之间的差模阻抗。永磁同步电机的转子是永磁体，忽略其涡流损耗和磁饱和效应，因此在建模中同样没考虑转子的影响。

② 抗测量

电机阻抗测量采用共模和差模测量两种方式，测试设备Agilent4294A，测试频段为100kHz-100MHz，测试频点数201个。共模测量即测试电机三端口并联后和机壳间的阻抗，其测试阻抗表示为，如图2所示；差模测量即测试电机两端口并联后和第三端口间的阻抗，其测试阻抗表示为，如图3所示。

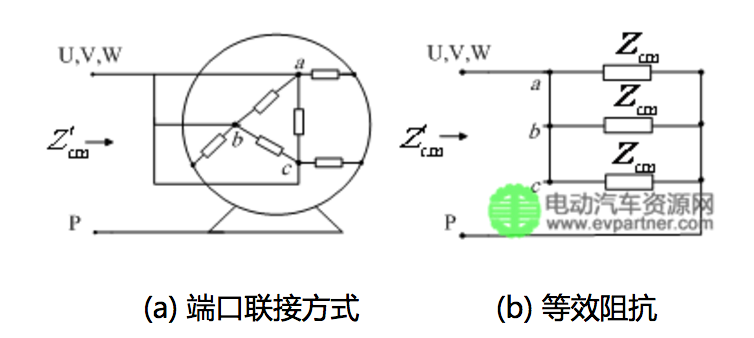
(a) 端口联接方式 (b) 等效阻抗
(a) Motor terminal connections (b) Motor equivalent impedance
图2共模阻抗

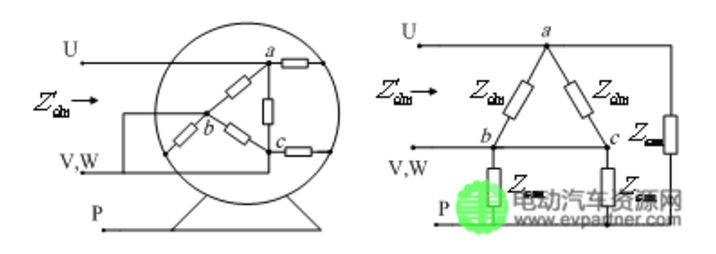
(a) 端口联接方式 (b) 等效阻抗
(a) Motor terminal connections (b) Motor equivalent impedance
图3差模阻抗

③数据处理

根据图2(b)和2(b)，测量阻抗和与绕组阻抗和的关系为：

(1.20)

(1.21)

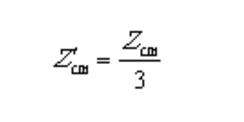
通过式(1.20)和(1.21)可以求得绕组阻抗和的表达式：

(1.22)

(1.23)

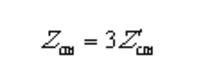
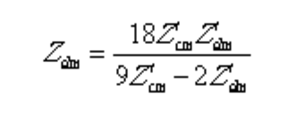
上节在建立星形联结电机建模过程中，使用了基于阻抗函数的矢量匹配法，本节将采用基于导纳函数的矢量匹配法拟合其等效电路。在此以求解的等效电路为例说明求解的整个过程。

表1 的矢量匹配法求解参数

Table.1 VF method for

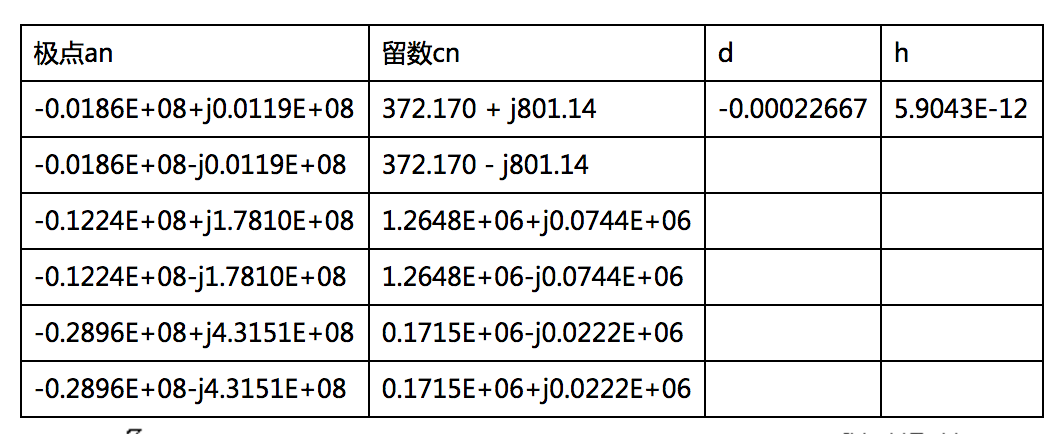
通过式(1.23)可得的阻抗特性数据，将获得的阻抗数据转换为导纳，即后，代入矢量匹配法程序，进行6阶拟合，得到导纳函数的极点和留数，如表1所示。

在Saber搭建阻抗和的等效电路模型，和的仿真与实测结果对比如图4所示。由图可知，用基于导纳函数的矢量匹配法拟合得到的电路参数能很好的吻合待建模阻抗的高频特性。在求解求解和等效电路的过程中，原始数据中包含的阻抗的实部、虚步信息，其仿真数据在幅值和相位上都有很好的拟合效果。

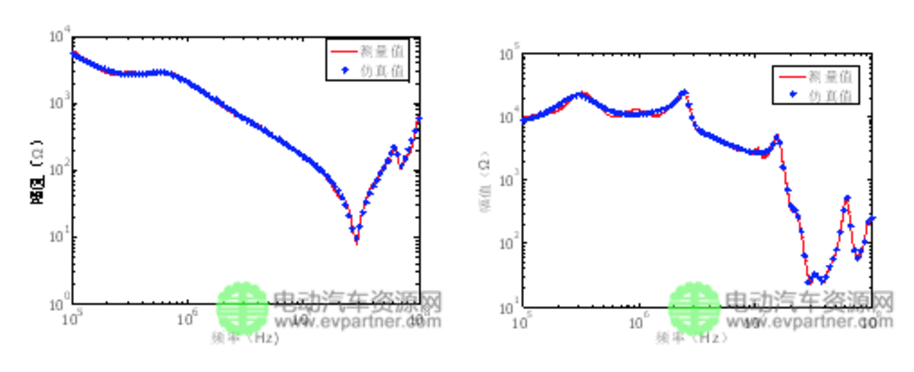
(a) 绕组共模阻抗 (b) 绕组差模阻抗
(a)The winding CM impedance (b) The winding DM impedance
图4 阻抗对比

③ 模型验证

将得到的和等效电路按图1的连接方式在Saber软件中搭建电机EMI高频模型。计算和在100 kHz~100 MHz的阻抗特性曲线，并与实际测量结果进行对比。阻抗曲线仿真和实测对比如图5、6所示，对比可以发现，测量阻抗的幅频特性和相频特性与仿真结果在整个频段范围内曲线吻合很好，进一步验证了矢量匹配法的正确性和准确性。

(a) 幅值 (b) 相位
(a) Amplitude (b) Phase
图5 仿真与实测结果

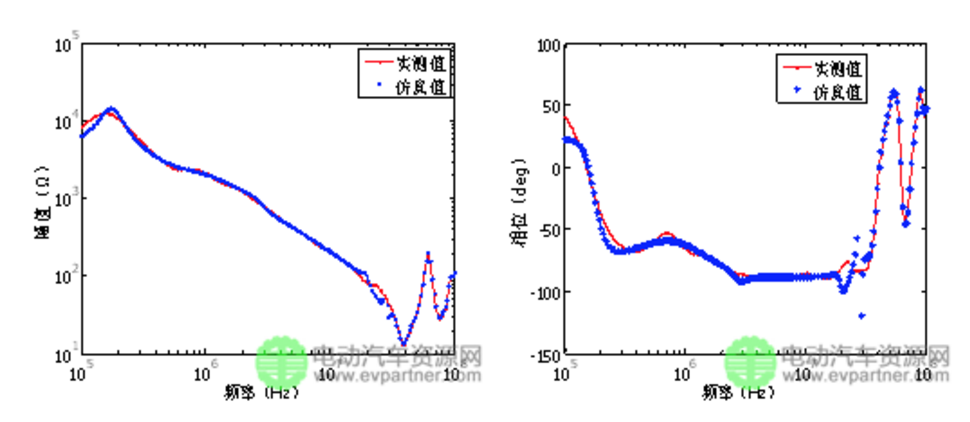
(a) 幅值 (b) 相位
(a) Amplitude (b) Phase
图6 仿真与实测结果

4 小结

本文研究了建立永磁同步电机高频电路模型的方法。介绍了矢量匹配法的基本原理，通过对网络函数极点和留数等参数的分析，分别推导出基于阻抗函数和导纳函数的等效电路建立过程，并应用于三角形联结的永磁同步电机高频电路的建模。永磁同步电机的建模过程归纳为：构建电机绕组高频模型的电路拓扑，通过共模测量和差模测量获得模型中共模阻抗和差模阻抗的频率特性；使用矢量匹配法将测试数据进行处理，计算阻抗（导纳）函数的极点留数等参数，随后转换为相应的等效电路。电机高频电路模型的时频域仿真结果和实测数据的对比，验证了利用矢量匹配法建立永磁同步电机高频模型的正确性和有效性。此外，该建模思路和方法同样可以用于其他种类的交流电机高频电路模型，具有一定的通用性。本研究内容为研究电机驱动传导电磁干扰和辐射电磁干扰问题打下基础，对建立驱动系统精确的传导和辐射干扰模型有重要意义。

参考文献

[1] Gustavsen B, Semlyen A. Rational Approximation of Frequency Domain Responses by Vector Fitting [J]. IEEE Trans. on Power Delivery, 1999, 14 (3):1052-1061.

[2] Zheng Y M, Wang Z J. Determining the Broadband Loss Characteristics of Power Transformer Based on Measured Transformer Network Functions and Vector Fitting Method [J]. IEEE Trans. on Power Delivery, 2013, 28 (4):2456-2464.

[3] Tang M, Sun J, Guo J Z. Time-Domain Modeling and Simulation of Partial Discharge on Medium-Voltage Cable by Vector Fitting Method [J]. IEEE Trans. on Magnetics, 2014, 50 (2):7024604-7024604.

[4] Joel K, Chirs B, John M D, Andreas W. A New Circuit Augmentation Method for Modeling of Interconnects and Passive Components [J]. IEEE Trans. on Advanced Packaging, 2006, 29 (1):67-77.

本文转自： 永磁同步电机高频建模方法研究

点击这里，获取更多电机控制设计信息