当MEMS惯性测量单元(IMU)用作运动控制系统中的反馈传感器时,你,必须了解陀螺仪的噪声情况,因为,它会在所监视的平台上造成不必要的物理运动。
根据具体情况,针对特定MEMS IMU进行早期应用目标噪声估算时需要考虑多个潜在的误差源。在此过程中需要考虑的三个常见陀螺仪特性——其固有噪声、线性振动响应和对准误差。
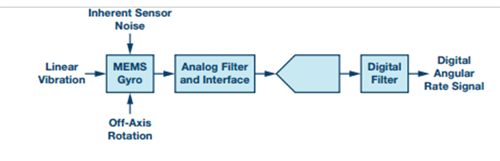
图 1的简单模型显示了会影响各误差源评估的几个特性:噪声源、传感器响应和滤波。此模型给出了对这些特性进行频谱分析所需的基准。
传感器固有噪声
传感器固有噪声代表的是陀螺仪在静态惯性和环境条件下运行时其输出中的随机振动。MEMS IMU数据手册通常会提供速率噪声密度(RND)参数来描述陀螺仪相对于频率的固有噪声。此参数通常使用单位°/s/√Hz,是预测特定滤波器配置固有噪声的关键。这里的公式给出了一种简单方法来估算与特定频率响应(噪声带宽)和RND相关的噪声。

当RND的频率响应遵循单极点或双极点低通滤波器曲线时,噪声带宽(fNBW)和滤波器截止频率(fC)将有如下的关系。

除了RND参数外,MEMS IMU数据手册有时会使用输出噪声等参数指定特定滤波器配置的陀螺仪固有噪声。输出噪声通常使用角速率标准单位(°/s),并使用均方根(rms)等统计术语来描述总噪声幅度。
线性振动
由于陀螺仪用于测量旋转角速率,因此其对线性运动的响应会引入测量误差。MEMS IMU数据手册通常通过“线性加速度对偏置的影响”或“线性加速度”等参数来描述对线性运动的这一响应,这些参数通常使用单位°/s/g。线性振动是一种重复的惯性运动,其幅度大小可通过位移(m)、线性速度(m/s)或线性加 速度(m/s2或g)表示。在特定的振动频率(fLV)下,位移(|dLV|)、速度(|vLV|)和加速度(|aLV|)之间的幅度关系如公式4所示。

当振动幅度以加速度(grms)表示时,与线性加速度参数相乘可估算陀螺仪测量中产生的噪声。例如,当ADIS16488A承受5 g (rms)的振动时,由于线性加速度等于0.009°/s/g,因此其陀螺仪中的 噪声估算值将为0.045°/s (rms)。

如图1所示,陀螺仪信号链常常包括滤波器,这有助于减少线性振动引起的噪声。以频谱项(幅度、频率)定义振动可在估算噪声贡献时考虑滤波器的影响。加速度频谱密度(ASD)函数是以频谱项表达振动的常见方式,通常使用单位g2/Hz。下面通过示例说明已知ASD和陀螺仪频率响应(HG)时估算噪声幅度的步骤:
1、ASD函数乘以陀螺仪频率响应的平方值;

2、利用帕塞瓦尔定理,通过在目标频率范围内对ASDF进行积分来计算“滤波振动曲线”中的平均功率;
利用帕塞瓦尔定理,通过在目标频率范围内对ASDF进行积分来计算“滤波振动曲线”中的平均功率;
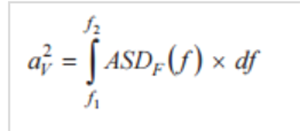
3、求取噪声功率估算值的平方根,然后与线性加速度系数(HLG)相乘即可计算出陀螺仪噪声幅度。

对准误差
运动控制系统通常会建立惯性参考系,其中包含三个相互垂直90°的轴。这三个轴为MEMS IMU中的各个传感器提供方位参考。理想情况下,陀螺仪的各个旋转轴将与系统参考系中的轴完全对齐,将IMU安装到平台上之后,其将监视运行情况。这种情况下,在惯性参考系中围绕其中一个轴旋转,只有该轴的陀螺 仪会生成响应。实际操作中,无法实现这种效果,因为机械缺陷必定会造成一些对齐误差,从而导致离轴陀螺仪响应惯性参考系中围绕一个轴的旋转运动。量化此响应需要一些三角恒等式,并谨慎定义陀螺仪的对齐误差。
每个陀螺仪的对齐误差均具有两个分量,分别定义其相对于惯性参考系中另一个轴的对齐误差。例如,对于图2中的系统,θXZ代表x轴陀螺仪相对于z轴的对齐误差。此对齐误差定义有助于建立公式以计算离轴陀螺仪对系统惯性参考系中围绕另一个轴旋转运动的响应。公式中给出了一个示例,其量化了x 轴陀螺仪相对于z轴的对齐误差(θXZ)和围绕z轴旋转(ωZR)而产生的响应(ωGX)。

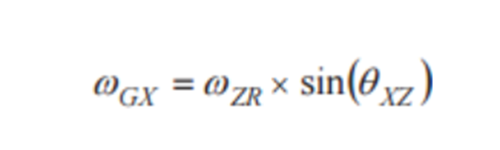
MEMS IMU通常具有两种类型的对齐误差,它们相互关联,但在系统级建模中具有不同应用——轴到封装和轴到轴:
“轴到封装对齐误差”描述陀螺仪相对于器件封装上特定机械特性的对齐情况。将IMU安装到系统后,如果系统无法支持惯性对齐,则轴到封装对齐误差将成为整体对齐误差的主要因素之一。系统与 IMU的机械接口的机械缺陷也会增加整体对齐误差;
“轴到轴对齐误差”描述各个陀螺仪旋转轴相对于其他两个陀螺仪的相对对齐精度。在系统可以实现简单的对齐过程时,此参数影响最大,此时通常沿系统的惯性参考系中的一个轴直线移动整个组件(IMU已安装在系统平台上),同时需要观察传感器。
如果对齐误差不是IMU规格的一部分,则通过评估器件封装中主要机械特性的物理容差就可以估算这些误差。例如,以下情况会引入0.5°的对齐误差:
4 mm × 4 mm LGA封装上的焊接回流工艺具有35 μm的安装误差;
PCB上相距20 mm的两个安装孔之间具有0.175 mm的容差。
案例研究
为了说明这些原理,请看以下示例,其中估算ADIS16488A中的陀螺仪噪声,该器件用于在以下配置/条件下运行的新型航电系统:
陀螺仪可用全带宽
振动(ASD(f)):0.122 g2/Hz;10 Hz到2000 Hz (总振动= 5 grms)
最大旋转速率 = ±100°/s,频率范围 = 5 Hz到50 Hz
全带宽配置匹配与ADIS16488A针对固有传感器噪声的0.135°/s(rms)的输出噪声规格相关的条件。对于振动贡献,图3给出了曲线说明ASD(f)以及滤波曲线ASDF(f)。ASDF(f)中的频率响应反映了与此IMU陀螺仪信号路径中双极点(404 Hz,757 Hz)低通滤波器相关的衰减曲线。

利用公式通过线性加速度参数乘以ASDF (f)曲线幅值2.24 g rms,可估算产生的噪声电平为0.02°/s (rms)。此噪声电平比通过公式5到的0.045°/s (rms)低55%,利用公式的方法未采用频谱项评估此噪声源。这种改善是采用频谱项定义振动曲线以获取值的一个示例。

通过如下公式可计算50 Hz频率下围绕z轴进行±100°/s旋转振荡时的x轴陀螺仪噪声。由于50 Hz恰好位于双极点滤波器的通带中,因此滤波器无法抑制此噪声源。此计算假设ADIS16488A的轴到轴对齐误差是主要误差源(也就是说,将IMU安装到系统后,全面部署时将包括简单的惯性参考系对齐过程)。
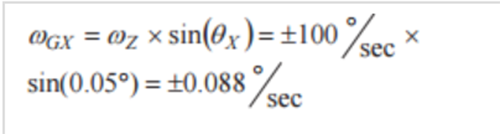
表1总结了ADIS16488A中来自各个因素的陀螺仪噪声。公式12给出了0.15°/s (rms)的整体噪声估算值(ωNOISE),表示表1中所有三个噪声源的平方和根值(RSS)。

上述这些方法利用相应数据手册中的常用参数信息以及对惯性条件的初步见解或估算,给出了评估MEMS陀螺仪信号中常见噪声源的简单流程。了解和评估这些噪声源有助于您确定重要的应用信息,指导IMU选择流程,还可以发掘改善机会(简单对齐,当IMU支持相应的轴到轴对齐误差级别时)以使用更经济的解决方案,反之则无法实现这种优势。